Fourierovy řady a Fourierova transformace

Úvod

Tuto stránku bych chtěl v budoucnu věnovat povídání o fourierovských řadách a transformacích a jejich uplatnění v astrofyzice, zejména ve spektroskopii, protože právě spektroskopie je hlavním polem zájmu členů stelárního oddělení Astronomického ústavu v Ondřejově.

Zatím tu prakticky nic není, až na pár následujících nesouvislých poznámek, protože nemám čas souvisle sepisovat nějaké povídání, na které bude potřeba, pravděpodobně, spíše několik set než několik desítek hodin.

V jistém smyslu lze tedy tuto stránku (alespoň v její sočasné podobě) chápat jako jakousi malou reklamu či upoutávku na větší povídání, které se tady jednou někdy objeví...

Co jsou Fourierovy řady a k čemu slouží?

Představme si, že chceme studovat (nebo třeba jenom aproximovat) chování nějaké poměrně složité periodické funkce. Ta nemusí být třeba ani spojitá (ovšem pozor! Smí být nespojitá nanejvýš na množině míry nula - ve smyslu Lebesgueovy míry), může mít nespojitou derivaci (tj. může být "hranatá") a vůbec se může chovat značně "nemravně" (v matematickém smyslu). Studovat takovou funkci, byť periodickou, nebude patrně nijak triviální. Proto se používají rozvoje takových "nemravných" funkcí do řad, které se již chovají rozumně. Jednou z takových metod je i rozvoj do Fourierovy řady. Je to (pokud v dalším textu nebude uvedeno jinak) rozvoj do trigonometrických řad, tj. do sinů a kosinů, na takovém intervalu, který pokrývá právě jednu periodu "mateřské" funkce - na jakýkoliv jiný interval je samozřejmě možné rozvoj periodicky rozšířit, protože i "mateřská" funkce se příslušným způsobem opakuje.

je důležité si uvědomit, že (bez jakékoliv újmy na obecnosti) se můžeme omezit na funkce s periodou

$<-\pi , \pi>$.
To je způsobeno tím, že jakoukoliv periodickou funkci lze vhodnou transformací upravit tak, aby se její perioda přepsala právě na ten interval $<-\pi , \pi>$. Vlastnosti funkce se přitom samozřejmě nijak nemění (koneckonců vzdálenost Měsíce od Země je také sama o sobě pořád stejná, bez ohledu na to, zda ji měříme v kilometrech, mílích, stopách, verstách nebo yardech).

Mějme tedy funkci

$f(x)$;
její rozvoj do Fourierovy řady na intervalu $<-\pi , \pi>$ lze symbolicky zapsat ve tvaru
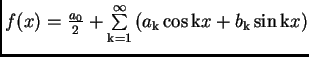
$ f(x)=\frac{a_0}{2}+\sum\limits_{{\rm k}=1}^{\infty} \left( a_{{\rm k}} \cos{{\rm k}x} + b_{{\rm k}} \sin{{\rm k}x} \right)$
čili
$f(x)=a_0 + a_1 \cos{x} + b_1 \sin{x} + a_2 \cos{2x} + b_2 \sin{2x} + a_3 \cos{3x} + b_3 \sin{3x} ...$
Zde výrazy
$a_{\rm k}$, $b_{\rm k}$
jsou Fourierovy koeficienty dané vztahy:
  • $a_0=\frac{1}{\pi}\int\limits_{-\pi}^{+\pi}f(x){\rm d}x$
  • $a_k=\frac{1}{\pi}\int\limits_{-\pi}^{+\pi}f(x) \cos{kx}{\rm d}x$
  • $b_k=\frac{1}{\pi}\int\limits_{-\pi}^{+\pi}f(x) \sin{kx}{\rm d}x$

    • Malý příklad

    Jako malý příklad zde prezentujeme rozvoj funkce

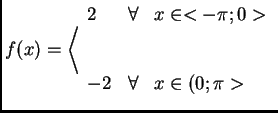
    $f(x)=\left< \begin{array}{lll} 2 & \forall & x \in <-\pi ; 0> \\ \; \\ \; \\ -2 & \forall & x \in (0; \pi> \end{array} \right. $
    Tato funkce je lichá, tedy koeficienty $a_{\rm k}$ jsou identicky rovny nule (díky tomu, že kosinus je funkce sudá). Celkový rozvoj zadané funkce do Fourierovy řady má tvar:
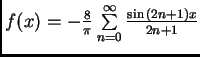
    $ f(x)=-\frac{8}{\pi}\sum\limits_{n=0}^{\infty}\frac{\sin{(2n+1)x}}{2n+1}$

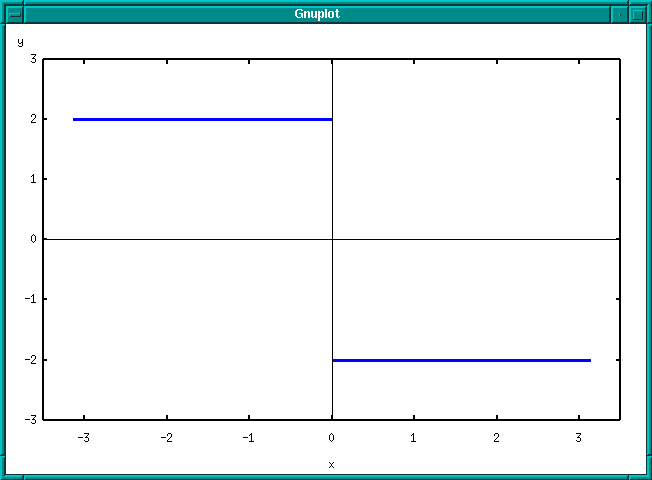
    Průběh funkce je zobrazen na obrázku:




    V následujícím přehledu ještě předkládáme obrázky, ze kterých je patrné, jak se postupně součty Fourierovy řady blíží k původní funkci.:

  • První součet, n=0
  • Druhý součet, n=1
  • Pátý součet, n=4



    • Druhý malý příklad

    Jako druhý malý příklad zde ukážeme Fourierův rozvoj funkce

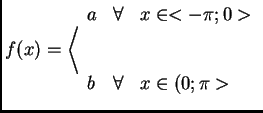    $f(x)=\left< \begin{array}{lll} a & \forall & x \in <-\pi ; 0> \\ \; \\ \; \\ b & \forall & x \in (0; \pi> \end{array} \right.$,
    kde předpokládáme $a>b$

    Tato funkce, na rozdíl od předchozího případu, není ani sudá ani lichá, nelze tedy předem říci, zda některé koeficienty Fourierova rozvoje budou nebo nebudou nulové. Teprve přímým výpočtem se přesvědčíme, že

  • $a_0=a+b$
  • $a_{\rm k}=0\;,\;k=1,2,...$
  • $b_k=\left< \begin{array}{lll} 0 & \forall & k \; {\rm sud^[.B~Né} \\ \; \\ \par\frac{2}{\pi}\frac{b-a}{k} & \forall & x \; {\rm lich~Né} \end{array} \right.$

    • Fourierův rozvoj této funkce je

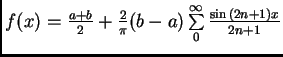
    $f(x)=\frac{a+b}{2}+\frac{2}{\pi}(b-a)\sum\limits_{0}^{\infty} \frac{\sin{(2n+1)x}}{2n+1}$

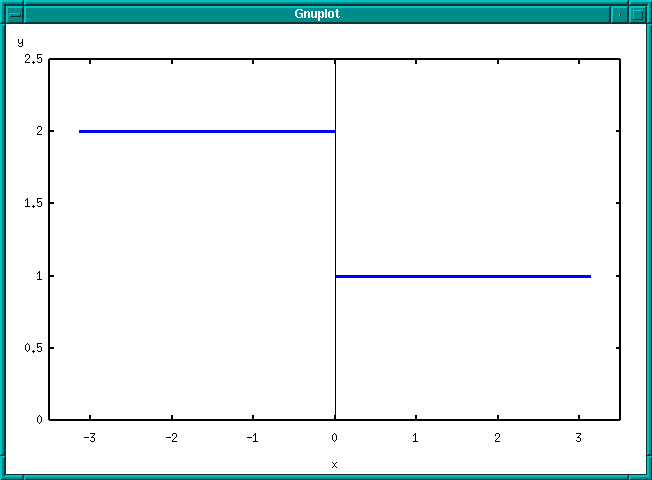
    Funkce má tvar




    Podobně jako v předchozím případě i zde podáváme v přehledu obrázky, ze kterých je patrné, jak se postupně částečné součty Fourierova rozvoje blíží k "mateřské" funkci:

  • První souččet, n=0
  • Druhý souččet, n=1
  • Šestý součet, n=5






    • Velmi zajímavý příklad

    Jako další příklad se již budeme věnovat trochu zajímavějšímu případu: pokusíme se PARABOLU $f(x)=x^2$ rozvinout do Fourierovy řady. Opět budeme pracovat na intervalu $<-\pi , \pi>$.

    Funkce $f(x)=x^2$ je sudá, tj. koeficienty jsou:

  • $a_0=\frac{2}{3}\pi^2$
  • $a_k=(-1)^k\frac{4}{k^2}\;\;k=1,2,3...$

    • Výsledný tvar Fourierova rozvoje je tedy:

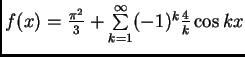
    $ f(x)=\frac{\pi^2}{3}+\sum\limits_{k=1}^{\infty}(-1)^k\frac{4}{k}\cos{kx}$

    Funkce má tvar:




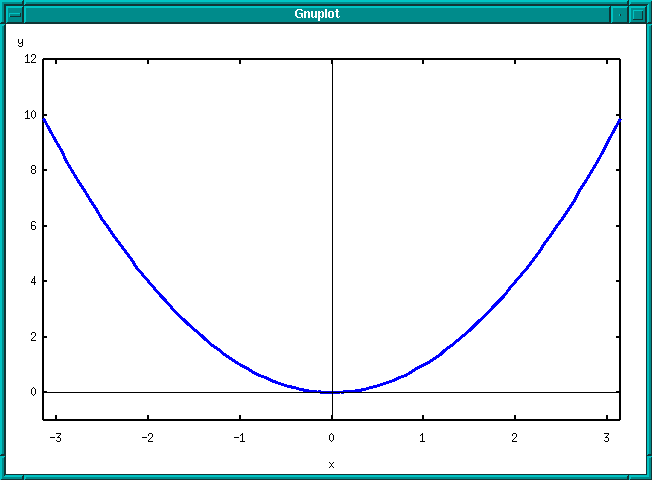
    a částečné součty jsou zobrazeny v následujícím seznamu:
  • První součet, n=0
  • Druhý součet, n=1
  • Třetí součet, n=2
  • Desátý součet, n=9



    • Další velmi zajímavý příklad

    Další zajímavý příklad, který zde budeme studovat, je rozvoj funkce

    $f(x)=x$
    do Fourierovy řady na intervalu (jak jinak...) $<-\pi , \pi>$

    Tato funkce je na zvoleném intervalu spojiná, lichá a nemá extrémy. Vzhledem k tomu, že je lichá, bude $a_{\rm k}=0\;\;k=0,1,2,3...$. Výpočtem dostaneme $b_{\rm k}=2(-1)^{k+1}\;\frac{1}{k}\;\;k=1,2,3...$

    Fourierův rozvoj této funkce tedy má tvar:

    $x=2\left[\sin{x}-\frac{1}{2}\sin{2x}+\frac{1}{3}\sin{3x}-\frac{1}{4}\sin{ 4x}+ ...+\frac{(-1)^{n+1}}{n}\sin{nx}+... \right]$

    Funkce má tvar




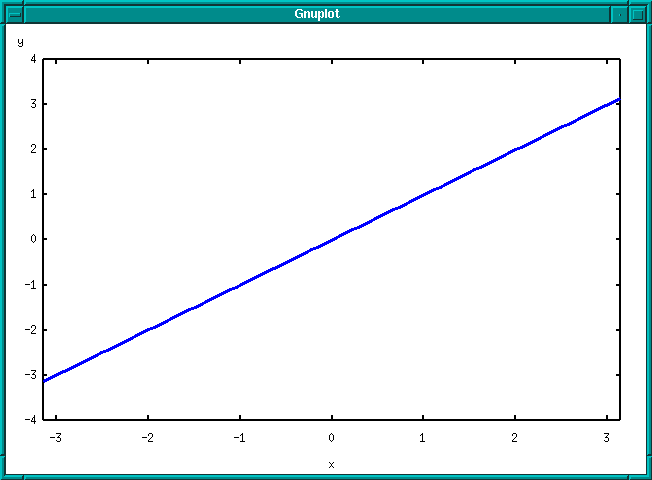
    Současně na následujícím obrázku předkládáme první a devátý částečný součet Fourierovy řady:

  • První a devátý součet k=9

    • Exponenciála

    Posledním příkladem, který tu budeme prezentovat, je rozvoj exponenciály do Fourierovy řady. Pracovat budeme opět na našem obvyklém intervalu $<-\pi , \pi>$. Mějme tedy exponenciálu danou vztahem:

    $f(x)=e^{ax} \;\; a \neq 0$

    Koeficienty Fourierova rozvoje jsou:

  • $a_0=\frac{2}{a \pi} \sinh{a \pi}$
  • $a_{{\rm k}}=(-1)^k \frac{1}{\pi}\;\frac{2a}{a^2+k^2}\sinh{a \pi}$
  • $b_{{\rm k}}=(-1)^{k-1}\frac{1}{\pi}\;\frac{2k}{a^2+k^2}\sinh{a \pi}$

    • Fourierův rozvoj tedy je:

    $ e^{ax}=\frac{2}{\pi}\sinh{a\pi}\Left[ \frac{1}{2a}+\sum\limits_{k=1}^{\infty} \frac{(-1)^k}{a^2+k^2} \left( a \cos{kx} -k \sin{kx} \right) \Right]$

    Funkce má tvar




    Současně předkládáme i ukázku postupné aproximace exponenciály. Jak vidno z přiložených obrázků, konvergence Fourierovy řady k "mateřské" exponenciále je poměrně velmi pomalá.

  • První částečný součet, k=1
  • Čtvrtý částečný součet, k=4
  • Sedmnáctý částečný součet, k=17
    •